Hjdcti

Riittävälla tarkkuudella kuvattu tiiliseinä.

Laskostumisesta johtuvia Moiré-kuvioita.

Laskostuminen (myös aliasoituminen, engl. aliasing) on signaalinkäsittelyssä signaalin kaistaleveyteen nähden liian pienestä näytteenottotaajuudesta johtuva signaalin vääristyminen. Kun analogisesta signaalista otetaan näytteitä näytteenotto- ja kvantisointipiirien avulla, näytteenottotaajuuden tulee Nyquistin teoreeman mukaisesti olla vähintään kaksinkertainen näytteistettävän signaalin taajuuteen verrattuna. Tätä niin sanottua Nyquistin taajuutta harvempi näytteenotto tai korkeampi signaalin kaistaleveys johtaa siihen, että yhdestä värähtelyjaksosta saadaan vähemmän kuin kaksi näytettä, eikä alkuperäistä signaalia enää voida palauttaa siitä otettujen näytteiden perusteella. Liian korkeataajuisesta signaalista otetut näytteet muodostavat samanlaisen näytejonon kuin näytteenottotaajuuden monikerran verran matalampi taajuuskin eikä näitä osasignaaleja voida erottaa toisistaan. Laskostumisessa muodostuu signaali, jonka taajuus on signaalitaajuuden ja näytteenottotaajuuden erotus.^[1]

Tunnettu esimerkki laskostumisesta on lännenelokuvissa usein näkyvä kärrynpyörien näennäinen väärä pyörimisnopeus. Elokuvafilmille otetaan näytteitä 24 kuvaa sekunnissa. Kärrynpyörien nopeus on sellainen, että kahden kuvan välillä pyörä ehtii kiertyä useammankin puolavälin ja näennäinen ”puolataajuus” laskostuu väärälle nopeudelle.^[2]

Näytteenottotaajuuden monikerran verran toisistaan poikkeavia taajuuksia kutsutaan nimellä aliakset koska näitä taajuuksia vastaavat signaalit summautuvat näytteenotossa eikä niitä voida enää erottaa toisistaan näytteistyksen jälkeen. Laskostumisen välttämiseksi signaali on suodatettava ennen näytteistämistä niin, että signaalin kaistaleveys on alle puolet näytteenottotaajuudesta. Yleensä tämä tapahtuu alipäästösuodattimella, joka suodattaa Nyquist taajuutta korkeammat taajuudet pois. Tällöin niiden mahdollisesti sisältämä informaatio menetetään mutta suodatus estää niiden virheellisestä tallentumisesta muuten aiheutuvan vääristymän.

Radiotekniikassa laskostumisehdot ja Nyquistin teoreema saavat hieman erilaisen muodon käytettäessä kvadratuurinäytteistystä. Kvadratuurinäytteistyksessä signaali on kompleksinen ja jokainen näyte on kompleksiluku. Kompleksisille signaaleille voidaan määritellä myös negatiiviset taajuudet – kompleksinen siniaalto tavallaan sisältää signaalin pyörimissuunnan. Kompleksisten signaalien tapauksessa taajuuden ylittäessä korkeimman positiivisen taajuuden signaalin taajuus kiertyy negatiiviseksi taajuudeksi samaan tapaan kuin binääriluvut positiivisen lukualueen ylittyessä kiertyvät negatiivisiksi luvuiksi. Jotta laskostumista ei kvadratuurinäytteistystä käytettäessä tapahtuisi, näytteenottotaajuuden on oltava vähintään näytteistettävän signaalin kaistaleveyden suuruinen. Tällöinkin jokaisesta jaksosta otetaan vähintään kaksi näytettä koska jokainen kompleksinen näyte sisältää kaksi arvoa: reaali- ja imaginääriosan.

Näytteistys ja rekonstruktio |

Sininen käyrä kuvaa punaisen käyrän alinäytteistyksestä johtuvaa laskostunutta rekonstruktiota. Mustat pallot kuvaavat punaisesta signaalista otettuja näytteitä. Ne voidaan ajatella kuuluvan kumpaan tahansa piirretyistä sinikäyristä, eikä rekonstruktiossa voida erottaa kummasta käyrästä näytteet on otettu.

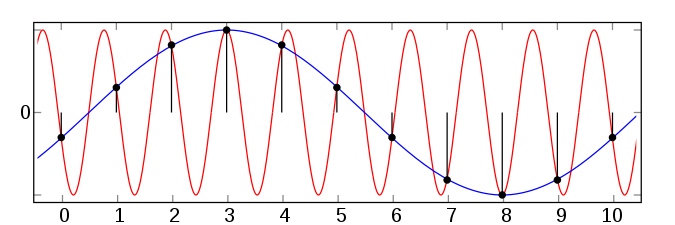
Nyquist-Shannonin näytteenottoteoreeman mukaan jatkuva funktio, joka ei sisällä suurempia taajuuksia kuin fdisplaystyle f, voidaan täydellisesti palauttaa näytteistä, jotka on otettu vähintään taajuudella 2fdisplaystyle 2f, (Nyquist-taajuus). Mikäli näytteenottotaajuus on matalampi signaali laskostuu kuten yllä olevassa kuvassa

Lähteet |

Kirjallisuutta |

• Oppenheim, Alan V.; Schafer, Roland W.: Digital Signal Processing. Prentice-Hall, Inc., 1975. ISBN 0-13-214635-5.

• Rabiner, Lawrence R.; Gold, Bernard: Theory and Application of Digital Signal Processing. Prentice-Hall, Inc., 1975. ISBN 0-13-914101-4.